Using the Unit Circle in Trigonometry

Reviewing for Calculus. Notes taken on Professor Leonard Trig 7 - How to Use the Unit Circle in Trigonometry, November 8-9, 2023.

[Let me apologize for the formatting of this – this looks better in Jupyter Lab than it will here. I’m not sure

Two different approaches to trig functions – show why they work.

One approach: trig functions relate an angle to two sides of a right triangle. (Usually one of the acute angles.) So need three things in every trig function.

Other approach:

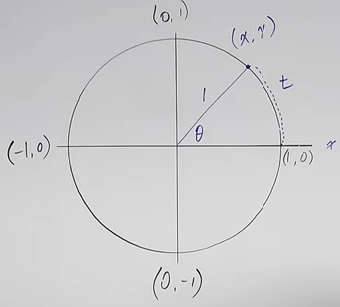
Remember for radians lectures

\[ s = r \theta \]

On unit circle, r = 1, and function becomes

\[ t = r\times \space \theta \]

or

\[ t = 1\times\theta \]

so ONLY on a unit circle, angle is same as arc length.

For radians, on unit circle, arc length = radius. If radius not one, doesn’t work.

\[ \sin t = \sin \theta = y \]

\[ \cos t = \cos \theta = x \]

\[ \tan t = \tan \theta = \frac{y}{x} = \frac{\sin\theta}{\cos\theta} \]

\[ \csc \theta = \frac{1}{y} \]

\[ \sec \theta = \frac{1}{x} \]

\[ \sec \theta = \frac{x}{y} \]

sin = y because y to x axis is vertical line, forming right triangle, etc.

So trig functions relate either the arc length or central angle to the point on the unit circle.

SOH CAH TOA

• SOH: Sin(θ) = Opposite / Hypotenuse

• CAH: Cos(θ) = Adjacent / Hypotenuse

• TOA: Tan(θ) = Opposite / Adjacent

Now filling out unit circle. Deal with

Quadrant Angles

Figuring out all six trig functions for angles (in radians), 0, \( \frac{\pi}{2} \), \( \pi \) \( \frac{3}{2} \pi \), \( 2 \pi \).

Note signs +/- for various functions in various quadrants.

Mnemonic: All Students Take Calculus for what sign is in four quadrants (I. All II sin III tan IV cos)

Relates to graphs of the trig functions

Can we determine trig functions from a point, say \( \lparen{-\frac{1}{2}, \frac{\sqrt{3}}{2}} )\)

Sin is y value, \( \frac{\sqrt{2}}{2} \) cos is x value, and tan is \( \frac{cos}{sin} = \frac{y}{x} - \sqrt{3} \). When reciprocate, should rationalize denominator.

Exercise: Find 6 trig function values for \( \frac{5\pi}{3} \)

I did some later functions on paper. I did mine before he did his – generally right. One mistake was on multiplying square roots. Note that this is correct:

\[ \sqrt(2) \space \times \space \sqrt(3) = \sqrt(6) \]

I thought I had to leave it as left hand side (unsimplifed).

Rest of video was mixed calculator / unit circles problems. Well, Jupyter is a calculator too, :) here we go.

import math

print("sin(28 degrees) = ", math.sin(math.radians(28)))
print("cot pi / 12 = ", 1 / math.tan(math.pi / 12))
print("sin 1 degree = ", math.sin(math.radians(1)))
print("sin 1 = ", math.sin(1))

sin(28 degrees) =  0.4694715627858908
cot pi / 12 =  3.7320508075688776
sin 1 degree =  0.01745240643728351
sin 1 =  0.8414709848078965

The above ended up being correct in terms of the lecture, so no dumb coding / typing mistakes. Just ended up watching the less problem, finding trig functions for a point (-3, 4), because I’m just reviewing for Calculus, I don’t want to major in trig. :)